Bluff problem of the day

[Call Me Wesley]

In these metaphysical circumstances, I will have the nuts (yes, I said 'nuts,' like in 'Snickers') 50% of the time, and be on a busted draw 50% of the time. Jake (that's not his real name, but let's call him that for now) will bet the nuts (100%) of the time, and bet with a bluffing hand (using mixed optimal strategies):

x = s / (1 + s)

Where s is equal to the percentage of the pot that Worm is bluff betting with and x is equal to the percentage of busted draws Worm should be bluffing with to bluff optimally.

Pot = 30 dollars. Bluff bet = 30 dollars.

s = 30(pot) / 30(bluff bet) = 1.

Jake should be bluffing with his busted draws:

x = 1 / (1 + s) = 50% Where s = 1

Assuming 4 trials, Jake has the nuts 2 times, and has a busted draw 2 times. (EV = Expected Value)

The purpose of optimal bluffing frequencies is to make the opponent (mathematically) indifferent between calling and folding. Optimal bluffing frequencies are based upon game theory and the Nash Equilibrium, and assist the player using these strategies to become unexploitable. By bluffing in optimal frequencies, you will typically end up breaking even on your bluffs (in other words, optimal bluffing frequencies are not meant to generate positive expected value from the bluffs alone). Rather, optimal bluffing frequencies allow you to gain more value from your "value bets," because your opponent is indifferent between calling or folding when you bet (regardless to whether it's a value bet or a bluff bet).

Now, with the Hilbert–Pólya conjecture, as you all know, I'd be able to find a self-adjoint operator, from the existence of which the cards in my opponent hands would amount to Flush ζs would follow when one applies the criterion on real eigenvalues, which means that I have $ 5 left.

Let's take a closer look at it:




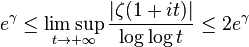
According to Ludwig Holtzmann, I could double my nuts, increasing my initial amount of ζs to ζs2. Which would enable me to buy a few Snicker bars.

My question therefore is, shall I wear these when bluffing?